Other than the
Generating and
Overcoming cycles, and the five
relationships, ancient China invented a method of categorizing and manipulating the five elements in a strict analytical system.
Zhi (Branches) of the Earth
Ancient Chinese invented a cycle of 12 items -- mirroring other ancient civilizations' love for categories based on the number 12 -- that map roughly to the
Five Elements. This cycle is of paramount importance in the study and application of the
Five Elements as it provides a
calculus for analysis of the five elemental forces.
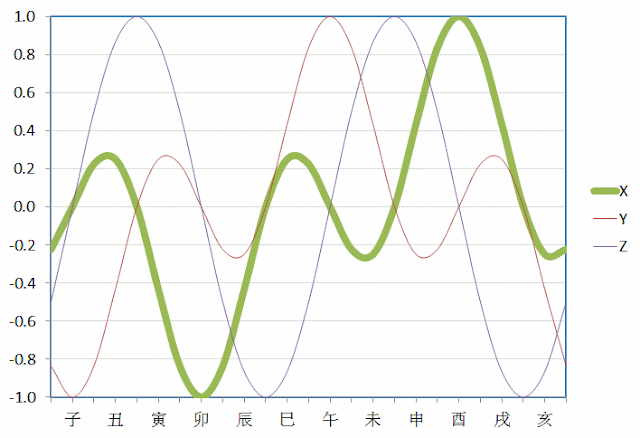
The cycle is the "Zhi" cycle -- "Zhi" meaning "branch":
子 (water), 丑 (earth),
寅 (wood), 卯 (wood), 辰 (earth),
巳 (fire), 午 (fire), 未 (earth),
申 (metal), 酉 (metal), 戌 (earth),
亥 (water)
The cycle is typically depicted in a circle, mapping the four elements water/fire/metal/wood on two axes:
As can be seen, the 12 items in the
Zhi cycle maps roughly to the four compass directions (north/south/east/west) according to the elements they refer to, with north (being cold) mapped to water, south (being hot) mapped to fire, east mapping to wood and west mapping to metal.
Notice a similarity mapping the
Five Elements with
the
Bagua trigrams in a
previous entry.
For reasons to be detailed below, this should be named the "simplistic" model.
Gan (Trunks) of the Heavens
At an unknown time in ancient China, another cycle of 10 items, again mapping roughly to the
Five Elements, was invented and termed the "Gan" cycle -- "Gan" meaning "trunk":
甲 (wood), 乙 (wood),
丙 (fire), 丁 (fire),
戊 (earth), 己 (earth),
庚 (metal), 辛 (metal),
壬 (water), 癸 (water)
The items in this cycle are mapped to the
Five Elements in a more predictable manner, with two mapping to each element in
Generating Order.
Gan/Zhi Combo
The 10 items in the
Gan cycle is usually combined, in sequence, with the 12 items in the
Zhi cycle to form a
Gan-Zhi combo with a period of 60, starting from 甲子 to癸亥. This 60-period cycle is usually called one
Jiazi (甲子) and is typically used to refer to 60 years.
The
Gan-Zhi combo is used primarily to label dates, with one combo used to label year, month, day, and hour respectively. These four-combo (year, month, day, hour) unique identifies a date/time within a long time span and forms the basis of the
Four Pillars (or
Eight Characters) system of fortune-telling.
The Zhi Cycle in Detail
As will be seen later, the
Zhi cycle plays a much more critical role in Chinese fortune-telling than the
Gan cycle, even though it is more complex (or perhaps due to its complexity).
The 12 items in the
Zhi cycle can be combined in various
patterns (a property missing from the
Gan cycle), the most important being the
3-Fusion (三會) and
3-Union (三合) patterns. These patterns essentially are
rules for applying the calculus on analysis of the
Five Elements.
Five Elements Phase Space Representation
The 12
Zhi items has a simple mathematical representation. Essentially, we we can take the following three-dimensional phase space model:
and treat each of the 12
Zhi items as
vectors lying on the water/fire/wood/metal plane.
By mathematical convention, we can term the wood/metal axis the "X-axis" with wood being the negative direction and metal being the positive direction, the water/fire axis the "Y-axis" with water being the negative direction and fire being the positive direction, and earth the "Z-axis" with up being positive (i.e. dry earth) and down being negative (i.e. wet earth).
Zhi Components
Each item in the
Zhi cycle can be decomposed into
component Gans (usually named the "hidden
Gan's" or 地支藏干) as follows:
子: 癸 (water)
丑: 己 (earth), 癸 (water), 辛 (metal)
寅: 甲 (wood), 丙 (fire), 戊 (earth)
卯: 乙 (wood)
辰: 戊 (earth), 乙 (wood), 癸 (water)
巳: 丙 (fire), 戊 (earth), 庚 (metal)
午: 丁 (fire), 己 (earth)
未: 己 (earth), 乙 (wood), 丁 (fire)
申: 庚 (metal), 戊 (earth), 壬 (water)
酉: 辛 (metal)
戌: 戊 (earth), 辛 (metal), 丁 (fire)
亥: 壬 (water), 甲 (wood)
On the surface, this makes sense if we treat each
zhi as a
vector on the
Five Elements Phase Space. The components are simply projections of each
zhi vector on the primary axes.
However, upon careful analysis, one can see a significant
problem with this interpretation -- the components elements are
intermixed with each other and do not clearly fall into their natural
compass directions. For example, 寅 and 戌, while being on the side of
water, has fire as component. This strange behavior is essentially the same for the eight
zhi vectors not pointing to strict compass points. This fact highlights the major short-coming of the "simplistic" model, which is planar on the X-Y plane.
The Standard Model
The presence of earth in most of the
zhi vectors also strongly indicate that these vectors do
not lie in the X-Y plane, and must have components in the Z-direction. Therefore, it is obvious that the "simplistic" model cannot be a true representation of the
Zhi cycle.
To correct the vector positions according to their components, the diagram should look like this:
Notice that this pattern is more complex than the "simplistic" representation which maps each
zhi vector in the X-Y plane along equal points on a circle.
The 3-Fusion (三會) Pattern
The
3-Fusion (三會) pattern is simple: three
Zhi together, when they occupy the three natural positions for a compass direction, combine to form a strong representation of the element. For example, the three
zhi items 亥, 子 and 丑 all lie in the south, with the first two mapping to water and the third mapping to earth. These three
zhi's combine to form a
3-Fusion patter for water, and are interpreted, taken together, as representing an extremely large magnitude for the water element.
Similarly, 寅, 卯, 辰 form the
3-Fusion pattern for wood, 巳, 午, 未 form the
3-Fusion pattern for fire, and 申, 酉, 戌 form the
3-Fusion pattern for metal:
The
3-Fusion patterns are easy to understand and model in modern mathematical language. A
3-Fusion pattern simply represents projections on the primary axis of the three
zhi vectors are in the same direction, therefore adding/reinforcing each other, with projections to the other axis on the X-Y plane cancelling each other.
For example, the vectors for the three
zhi's 寅, 卯 and 辰 all have negative projections on the
X-axis, so the magnitude of wood is essentially strengthened. On the other hand, projection of 寅 on the Y-axis is positive while the projection of 辰 on the Y-axis is negative, with magnitudes exactly cancelling each other (projection of 卯 on the Y-axis is zero).
This property of the
3-Fusion pattern works for both the "simplistic" model and the Standard Model.
Therefore, treating each
Zhi item as a vector lying on the X-Y plane in the
Five Elements Phase Space works well to interpret the
3-Fusion pattern, with the resulting vector lying on either the X or Y axis.
For obvious reasons, there is no
3-Fusion pattern for earth.
The 3-Union (三合) Pattern
The
3-Union (三合) pattern is also extremely important and cited even more frequently than the
3-Fusion pattern in literature. A
3-Union combo is considered to be weaker than a
3-Fusion combo for any element, but magnitude-wise still much stronger than a single vector representing that element.
It is, however, quite strange in that the three
Zhi vectors each lie on different sides, forming a unilateral triangle in the "simplistic" model.
When plotted on the
Five Elements Phase Space model according to the Standard Model, they represent three vectors on the
outlying of each compass direction:
The three vectors for each
3-Union pattern again combine to result in a vector lying purely on either the X or Y axis, with all other components cancelling out. The resultant vector is of smaller magnitude than the resultant vector of a
3-Fusion pattern due to two vectors being on the
outlying region of each compass direction.
Again, for obvious reasons, there is no
3-Union pattern for earth.
2-Fusion and 2-Union Patterns
There are defined in classical Chinese fortune-telling literature of the
2-Fusion (半會) and
2-Union (半合) patterns, though not as useful as the full
3-Fusion and
3-Union patterns.
These two "half patterns" are weaker than the
3-Union, but nevertheless still indicate a somewhat strengthening of the representative element. A "half pattern" is formed with only two out of the three items in
3-Fusion and
3-Union.
The Standard Model works well in representing
2-Fusion and
2-Union.
Other Patterns
There are other patterns used regularly in fortune-telling, though most are not as prevalent as the
3-Fusion and
3-Union patterns.
The most significant one among them must be the
Cancellation pattern -- each item in the
Zhi cycle
cancels an equivalent item directly opposing it (i.e. an item located 180 degrees from it). In fortune-telling applications,
cancellations are usually interpreted as either completely negating a good aspect (or making it bad), or strengthening an already bad aspect. When mapped to the Standard Model and the
Five Elements Phase Space, it has one straight meaning -- that two
zhi vectors point to opposite directions and exactly
cancel each other in magnitude. That this will negate a good aspect (i.e.
zhi vector pointing to a beneficial direction) is easily understandable. When
cancellation occurs, the resultant vector usually ends up with a smaller magnitude (as the magnitudes of two vectors completely cancel each other out), and as will be seen in later entries, a small resultant vector magnitude usually signifies weakness and is most commonly a "bad thing".
There is the
6-Harmony (六合) pattern which is used also quite frequently. This pattern, however, does not lend itself to a ready explanation in the Standard Model.
Other miscellaneous patterns such as the
6-Harming (六害), the
6-Punishments (六刑) etc. also have the same problem.
What About Earth?
Earth is a strange beast in the
Zhi cycle (but not in the
Gan) cycle. Under the Standard Model, it alone represents an entire axis in the
Five Elements Phase Space.
This special treatment of earth also strongly suggests that, although the
Zhi cycle is a calculus on the
Five Elements, they are
not the same Five Elements as depicted in the
Gan cycle! As a results, it is strongly hinted that there are
two different
Five Elements systems, and there must be ways to model their interactions with each other.
For example, the Standard Model does not model the exact
generating and
overcoming cycles of the
Five Elements. Instead, mathematically, pairs of elements are opposite of each other and cancels each other -- i.e. water with fire, wood with metal -- at least these are
overcoming relationships. Their interactions with each other are limited, as they represent different axes. For instance, while water
generates wood in the
Five Elements, water and wood has no direct interactions in the Standard Model.
In practical applications of the
Gan and
Zhi cycles to analyze
Five Elements, it is common to primarily consider
patterns formed by the
zhi vectors first and foremost, disregarding the
generating/
overcoming impacts. Only when all such patterns are considered should the resultant vectors and stand-alone vectors (which do not participate in any pattern) are considered via the elements in a classical
Five Elements manner.
As will be seen in later entries, the Standard Model combines
all zhi vectors into
one resultant vector (which should only represent up to three elements, mapping to the three axes in the
Five Elements Phase Space). These three elemental components are then combined with the
Gan items, if any, and interpreted via
generating/
overcoming analysis.
Fixing the Z Component
The
3-Union and
3-Fusion patterns strongly suggest that the Z-axis components of the vectors forming those patterns will cancel out in magnitude and direction, meaning that there are only two possible ways to fix the third dimension on each
zhi vector and still be symmetric. The first possibility, the preferred, has the
3-Union and
3-Fusion patterns resulting in vectors with no Z components (red = negative Z, green = positive Z):
Another possibility has the
3-Union and
3-Fusion patterns resulting in vectors with non-zero Z components (red = negative Z, green = positive Z):
The first possibility is preferred as it is completely symmetric, but the second possibility also has certain attractiveness -- in particular, they can be generated by a great circle on a quaternion hypersphere, as show in the next entry!