"Jing Fang" Style of Fortune Telling Based on Hexgrams and Five Elements

The Jing Fang Method

The prominent scholar Jing Fang (京房) of the Han dynasty (77-37BC) revolutionized fortune telling based on the 64 hexgrams by marrying them with the concept of the Five Elements.

His method is:

1. Generate a trigram by the coin substitute method; this is the base hexgram (see this entry)
2. Create the alternate hexgram by flipping all lines marked with O or X
3. The base hexgram is used to predict the general state of an event or issue, while the alternative hexgram is used to predict the outcome of an event or issue
4. Identify the houses of each hexgram
5. The element of the base trigram of the house of the base hexgram is the source (原神)
6. The element of the base trigram of the house of the alternative hexgram is used to predict the final outcome
7. Allocate a Zhi (from the 12-Zhi cycle) to each line of both hexgrams based on an algorithm (the reader can look this up)
8. Take the appropriate element (based on the event or issue being predicted) as the target (用神)
9. Make predictions based on the twelve zhi items

When expressed in the language of the Standard Model, step 8-9 become:

1. For each zhi item allocated to each line of both hexgrams, find its corresponding 3D vector in the Five Elements Phase Space based on the Standard Model
2. Create a resultant vector by combining the six vectors of the base hexgram
3. Create a resultant vector by combining the six vectors of the alternative hexgram
4. Identify the target (用神) element based on the source (原神)
5. Identify the magnitude of the target element by projecting the resultant vector of the base hexgram -- this generally predicts the strength of the target, or the event/issue being predicted
6. Identify the magnitude of the target element by projecting the resultant vector of the alternative hexgram -- this generally predicts the strength of the final outcome of the event/issue being predicted
7. The interactions of both resultant vectors also have implications on whether the final outcome will be favorable or unfavorable -- for example, if the resultant vector of the alternative hexgram is much weaker than the other

Observations

Using the Zhi Formula and the Standard Model takes most of the guesswork out of applying the Jing Fang Method of fortune telling.

There are, however, some unknowns, for example the rationale behind the algorithm of allocating zhi items to each line of a hexgram. Also, practitioners of the Jing Fang method can usually make fine-grained predictions, including specific details, based on the complex interactions of the 12 zhi items -- these cannot be easily generated by the conceptualized Standard Model which reduces all interactions to a single vector embedded in phase space.

The Jing Fang Method is also the first under this study that utilizes the concept of relationships to make predictions on a particular event or issue.  This is actually only an application of the general concept of mapping a base (e.g. the Self House 命宮 in Ziwei Numbers, or the Day Pillar 日柱 in the Four Pillars) and then looking for the correct element or house for the event/issue under question based on relationships. More of this can be seen in future entries when studying other systems of fortune telling, although in many cases, a uniform 60° is used instead of the 72° in the Five Elements basic model.

Practical Example

This example is chosen at random from the book 周易与预测学 (The I-Ching and The Science of Predictions) by 邵伟华.  A prediction was seeked for the illness of asker's wife.

The base hexgram obtained was 比 and the alternate hexgram was 謙, meaning the second and forth lines of the base hexgram were flipped to form the alternate hexgram.

The houses of each hexgrams: 比 is of the house of 坤 (an earth 土 house) and 謙 is of the house of 兌 (a metal 金 house).  Therefore, the source element is earth (土).

As the event being asked is related to the asker's wife, and within the five relations a wife falls under the overcomed, thus the target element (用神) is the element overcome by the source element, or water (水).

Therefore, right away, we have the element of the alternate hexgram being a benefactor (i.e. generator) of the target element -- a particularly optimistic result generally, indicating that it is likely the event will end optimistically (remember the alternate hexgram indicates the outcome of a prediction).

The zhi vectors under the Standard Model for the base hexgram are:

1st Line: 子 (water) = (0, -1, 0)
2nd Line: 戌 (earth) = (+0.43, +0.25, -0.87)
3rd Line: 申 (metal) = (+0.43, -0.25, +0.87)
4th Line: 卯 (wood) = (-1, 0, 0)
5th Line: 巳 (fire) = (+0.25, +0.43, -0.87)
6th Line: 未 (earth) = (-0.25, +0.43, +0.87)

Not considering adjustments made due to season and location (e.g. hotter seasons magnify fire while colder seasons magnify water, spring magnifies wood while autumn magnifies metal), the resultant vector is (-0.14, -0.14, 0), meaning that it is weakly negative (i.e. wood) on the X-axis and weakly negative (i.e. water) on the Y-axis.  The Z-axis component is zero.

As the target element of the event is water, we can judge from the resultant vector of the base hexgram that it is weakly beneficial -- although not strongly but at least not detrimental. This indicates that the wife is weak from illness, but that the illness is likely not to be serious or life-threatening.

The zhi vectors for the alternate hexgram are:

1st Line: 酉 (metal) = (+1, 0, 0)
2nd Line: 亥 (water) = (-0.25, -0.43, -0.87)
3rd Line: 丑 (earth) = (+0.25, -0.43, +0.87)
4th Line: 申 (metal) = (+0.43, -0.25, +0.87)
5th Line: 午 (fire) = (0, +1, 0)
6th Line: 辰 (earth) = (-0.43, -0.25, -0.87)

The resultant vector is (+1, -0.36, 0) -- strongly metal (X-axis) and mildly water (Y-axis), but again no earth.

As the element of the alternate hexgram has mild magnitude in the target element axis, this indicates that the outcome of the prediction should be optimistic, and generally more positive than the original state.

In other words, the wife is expected to recover from a non-life-threatening illness.

Gan/Zhi Con't - Formula for The Zhi Cycle

The Standard Model

Starting from the Standard Model -- the version that yields zero magnitudes in the Z axis for 3-Fusion and 3-Union patterns:

It is now possible to compile the equation governing the Zhi cycle's trajectory in the Five Elements Phase Space. The transition from 丑 to 寅, for instance, flips the vector to the opposite side of the plane; same thing for 辰 to 巳, 未 to 申, 戌 to 亥.

This behavior can be successfully modeled by a vector that not only rotates through 360° in the X-Y plane, but also rotates into the Z dimension.

Vector Illustration

Consider a vector that rotates in the X-Y plane through the angle θ, while at the same time rotating by an angle φ about an axis in the X-Y plane that is perpendicular to the vector's projection into X-Y:

When φ > 90°, the vector flips to the opposite side of the X-Y plane, creating the behavior that we observe in the Zhi cycle.

Mapping the vector rotation with components of the Zhi cycle items, it is easy to come up with the fact that:

φ = 2θ

In other words, as the vector rotates 360° through the X-Y plane (representing one complete period of the Zhi cycle), the vector rotates into the Z dimension through 720° -- or two complete rotations.

The Standard Model Formula

Assuming a unit vector:

`x = cos phi sin theta = cos 2 theta sin theta`
`y = -cos phi cos theta = -cos 2 theta cos theta`
`z = sin phi = sin 2 theta`

The minus sign for y is simply there to cast water into negative and fire into positive, instead of the other less-intuitive way.

There is a minor adjustment required. In classical literature, the zhi items 子, 卯, 午, 酉 point to compass directions only in the middle of their segment.  For example, when the Zhi cycle is applied to mark time, the hour represented by 子 is 11:00pm on the previous night to 1:00am, with the mid-point being midnight.  Essentially, only at midnight is the vector for 子 coinciding with the Y axis.

Since each Zhi item occupies 30° in a complete circle, the Zhi cycle must therefore start with θ = -15° instead of θ = 0°.

Formula Behavior

The Zhi cycle when projected on the X-axis takes on the following values (as shown with the green line):

Negative is wood while positive is metal.  The 3-Fusion for wood (寅, 卯, 辰) and 3-Fusion for metal (申, 酉, 戌) are both clearly seen as the lowest trough and highest peak respectively. The lowest/higher points, together with the two sub-depression/sub-peaks surrounding them, form the 3-Union patterns for wood and metal respectively.

Projections on the Y axis (red line) shows similar behavior:

Projections on the Z axis (blue line) is a simple sine curve:

It can be seen immediately that, for all Zhi items with earth as component (i.e. all the items that do not point to pure compass directions) have component values at the mid-point of 0.87 -- almost 90% of the peak value.

This explains why, in classical literature, the earth components of these Zhi items cannot be ignored -- they are almost stronger than any other component -- while there are no earth components for the four Zhi items pointing to pure compass directions. For those items, the actual earth component takes on various values from positive to negative, while that component is zero at the mid-point.

Quaternion Interpretations

The rule φ = 2θ is interesting because, as θ goes from 0° to 360°, φ goes from 0° to 720° (or two complete revolutions). It is well known in geometry and topology that a rotation by360° in three dimensional space is not a symmetry operation (i.e. an object remains twisted), but 720° is symmetric (i.e. the object rotated is not twisted) -- a fact described by the mathematics of quaternions and spinors.

The Standard Model formula describes a curve on the three-dimensional quaternion hypersphere -- a "figure-eight" curve with two loops on both the northern and southern hemisphere. When the hypersphere (in blue) is looked upon from the top, the curve (in red) looks like:

The plane shows θ going from 0° to 360°, while the third dimension (through the plane) ranges from a rotation φ from 0° to 360° -- 0° is the north pole and 360° is the south pole. The red circle is actually two circles stacked on top of each other -- one in the northern hemisphere and one in the southern hemisphere. The trajectory follows a figure-eight path tracing through these two circles.

In the previous entry, it is mentioned that another possible mapping of the Z-axis:

It has fewer redeeming qualities than the Standard Model -- for example, the 3-Fusion and 3-Union patterns yield non-zero components in the Z-axis.  It is also less uniform to fit resulting vector trajectory.

However, this mapping can be described by a great circle on the quaternion hypersphere. But unless the great circle follows the longitudes and go through both poles, the four compass directions 子, 午, 卯, 酉 must also have non-zero components in the Z-axis.

No ancient Chinese texts associated any earth component for 3-Fusion, 3-Union and the four compass directions, except for 午 -- but this fact is explained in a future entry.

Other Interpretations

Considering the 720° rotation of φ, it is possible that the Standard Model formula can be described more elegantly via spinor algebra -- but I am not good enough a mathematician to do this.

Gan/Zhi (Trunks/Branches) - Calculus for the Five Elements

Other than the Generating and Overcoming cycles, and the five relationships, ancient China invented a method of categorizing and manipulating the five elements in a strict analytical system.

Zhi (Branches) of the Earth

Ancient Chinese invented a cycle of 12 items -- mirroring other ancient civilizations' love for categories based on the number 12 -- that map roughly to the Five Elements. This cycle is of paramount importance in the study and application of the Five Elements as it provides a calculus for analysis of the five elemental forces.

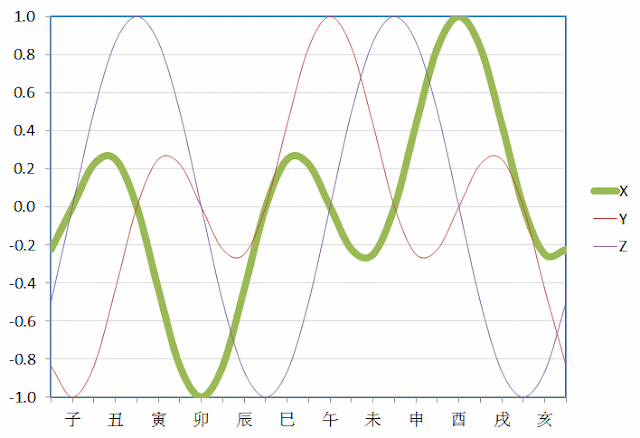
The cycle is the "Zhi" cycle -- "Zhi" meaning "branch":

子 (water), 丑 (earth),
寅 (wood), 卯 (wood), 辰 (earth),
巳 (fire), 午 (fire), 未 (earth),
申 (metal), 酉 (metal), 戌 (earth),
亥 (water)

The cycle is typically depicted in a circle, mapping the four elements water/fire/metal/wood on two axes:

As can be seen, the 12 items in the Zhi cycle maps roughly to the four compass directions (north/south/east/west) according to the elements they refer to, with north (being cold) mapped to water, south (being hot) mapped to fire, east mapping to wood and west mapping to metal.

Notice a similarity mapping the Five Elements with the Bagua trigrams in a previous entry.

For reasons to be detailed below, this should be named the "simplistic" model.

Gan (Trunks) of the Heavens

At an unknown time in ancient China, another cycle of 10 items, again mapping roughly to the Five Elements, was invented and termed the "Gan" cycle -- "Gan" meaning "trunk":

甲 (wood), 乙 (wood),
丙 (fire), 丁 (fire),
戊 (earth), 己 (earth),
庚 (metal), 辛 (metal),
壬 (water), 癸 (water)

The items in this cycle are mapped to the Five Elements in a more predictable manner, with two mapping to each element in Generating Order.

Gan/Zhi Combo

The 10 items in the Gan cycle is usually combined, in sequence, with the 12 items in the Zhi cycle to form a Gan-Zhi combo with a period of 60, starting from 甲子 to癸亥. This 60-period cycle is usually called one Jiazi (甲子) and is typically used to refer to 60 years.

The Gan-Zhi combo is used primarily to label dates, with one combo used to label year, month, day, and hour respectively.  These four-combo (year, month, day, hour) unique identifies a date/time within a long time span and forms the basis of the Four Pillars (or Eight Characters) system of fortune-telling.

The Zhi Cycle in Detail

As will be seen later, the Zhi cycle plays a much more critical role in Chinese fortune-telling than the Gan cycle, even though it is more complex (or perhaps due to its complexity).

The 12 items in the Zhi cycle can be combined in various patterns (a property missing from the Gan cycle), the most important being the 3-Fusion (三會) and 3-Union (三合) patterns. These patterns essentially are rules for applying the calculus on analysis of the Five Elements.

Five Elements Phase Space Representation

The 12 Zhi items has a simple mathematical representation.  Essentially, we we can take the following three-dimensional phase space model:

and treat each of the 12 Zhi items as vectors lying on the water/fire/wood/metal plane.

By mathematical convention, we can term the wood/metal axis the "X-axis" with wood being the negative direction and metal being the positive direction, the water/fire axis the "Y-axis" with water being the negative direction and fire being the positive direction, and earth the "Z-axis" with up being positive (i.e. dry earth) and down being negative (i.e. wet earth).

Zhi Components

Each item in the Zhi cycle can be decomposed into component Gans (usually named the "hidden Gan's" or 地支藏干) as follows:

子: 癸 (water)
丑: 己 (earth), 癸 (water), 辛 (metal)
寅: 甲 (wood), 丙 (fire), 戊 (earth)
卯: 乙 (wood)
辰: 戊 (earth), 乙 (wood), 癸 (water)
巳: 丙 (fire), 戊 (earth), 庚 (metal)
午: 丁 (fire), 己 (earth)
未: 己 (earth), 乙 (wood), 丁 (fire)
申: 庚 (metal), 戊 (earth), 壬 (water)
酉: 辛 (metal)
戌: 戊 (earth), 辛 (metal), 丁 (fire)
亥: 壬 (water), 甲 (wood)

On the surface, this makes sense if we treat each zhi as a vector on the Five Elements Phase Space. The components are simply projections of each zhi vector on the primary axes.

However, upon careful analysis, one can see a significant problem with this interpretation -- the components elements are intermixed with each other and do not clearly fall into their natural compass directions.  For example, 寅 and 戌, while being on the side of water, has fire as component. This strange behavior is essentially the same for the eight zhi vectors not pointing to strict compass points.  This fact highlights the major short-coming of the "simplistic" model, which is planar on the X-Y plane.

The Standard Model

The presence of earth in most of the zhi vectors also strongly indicate that these vectors do not lie in the X-Y plane, and must have components in the Z-direction. Therefore, it is obvious that the "simplistic" model cannot be a true representation of the Zhi cycle.

To correct the vector positions according to their components, the diagram should look like this:

Notice that this pattern is more complex than the "simplistic" representation which maps each zhi vector in the X-Y plane along equal points on a circle.

The 3-Fusion (三會) Pattern

The 3-Fusion (三會) pattern is simple: three Zhi together, when they occupy the three natural positions for a compass direction, combine to form a strong representation of the element.  For example, the three zhi items 亥, 子 and 丑 all lie in the south, with the first two mapping to water and the third mapping to earth.  These three zhi's combine to form a 3-Fusion patter for water, and are interpreted, taken together, as representing an extremely large magnitude for the water element.

Similarly, 寅, 卯, 辰 form the 3-Fusion pattern for wood, 巳, 午, 未 form the 3-Fusion pattern for fire, and 申, 酉, 戌 form the 3-Fusion pattern for metal:

The 3-Fusion patterns are easy to understand and model in modern mathematical language.  A 3-Fusion pattern simply represents projections on the primary axis of the three zhi vectors are in the same direction, therefore adding/reinforcing each other, with projections to the other axis on the X-Y plane cancelling each other.

For example, the vectors for the three zhi's 寅, 卯 and 辰 all have negative projections on the X-axis, so the magnitude of wood is essentially strengthened. On the other hand, projection of 寅 on the Y-axis is positive while the projection of 辰 on the Y-axis is negative, with magnitudes exactly cancelling each other (projection of 卯 on the Y-axis is zero).

This property of the 3-Fusion pattern works for both the "simplistic" model and the Standard Model.

Therefore, treating each Zhi item as a vector lying on the X-Y plane in the Five Elements Phase Space works well to interpret the 3-Fusion pattern, with the resulting vector lying on either the X or Y axis.

For obvious reasons, there is no 3-Fusion pattern for earth.

The 3-Union (三合) Pattern

The 3-Union (三合) pattern is also extremely important and cited even more frequently than the 3-Fusion pattern in literature. A 3-Union combo is considered to be weaker than a 3-Fusion combo for any element, but magnitude-wise still much stronger than a single vector representing that element.


It is, however, quite strange in that the three Zhi vectors each lie on different sides, forming a unilateral triangle in the "simplistic" model.


When plotted on the Five Elements Phase Space model according to the Standard Model, they represent three vectors on the outlying of each compass direction:

The three vectors for each 3-Union pattern again combine to result in a vector lying purely on either the X or Y axis, with all other components cancelling out.  The resultant vector is of smaller magnitude than the resultant vector of a 3-Fusion pattern due to two vectors being on the outlying region of each compass direction.

Again, for obvious reasons, there is no 3-Union pattern for earth.

2-Fusion and 2-Union Patterns

There are defined in classical Chinese fortune-telling literature of the 2-Fusion (半會) and 2-Union (半合) patterns, though not as useful as the full 3-Fusion and 3-Union patterns.

These two "half patterns" are weaker than the 3-Union, but nevertheless still indicate a somewhat strengthening of the representative element. A "half pattern" is formed with only two out of the three items in 3-Fusion and 3-Union.

The Standard Model works well in representing 2-Fusion and 2-Union.

Other Patterns

There are other patterns used regularly in fortune-telling, though most are not as prevalent as the 3-Fusion and 3-Union patterns.

The most significant one among them must be the Cancellation pattern -- each item in the Zhi cycle cancels an equivalent item directly opposing it (i.e. an item located 180 degrees from it). In fortune-telling applications, cancellations are usually interpreted as either completely negating a good aspect (or making it bad), or strengthening an already bad aspect. When mapped to the Standard Model and the Five Elements Phase Space, it has one straight meaning -- that two zhi vectors point to opposite directions and exactly cancel each other in magnitude. That this will negate a good aspect (i.e. zhi vector pointing to a beneficial direction) is easily understandable. When cancellation occurs, the resultant vector usually ends up with a smaller magnitude (as the magnitudes of two vectors completely cancel each other out), and as will be seen in later entries, a small resultant vector magnitude usually signifies weakness and is most commonly a "bad thing".

There is the 6-Harmony (六合) pattern which is used also quite frequently. This pattern, however, does not lend itself to a ready explanation in the Standard Model.

Other miscellaneous patterns such as the 6-Harming (六害), the 6-Punishments (六刑) etc. also have the same problem.

What About Earth?

Earth is a strange beast in the Zhi cycle (but not in the Gan) cycle.  Under the Standard Model, it alone represents an entire axis in the Five Elements Phase Space.

This special treatment of earth also strongly suggests that, although the Zhi cycle is a calculus on the Five Elements, they are not the same Five Elements as depicted in the Gan cycle!  As a results, it is strongly hinted that there are two different Five Elements systems, and there must be ways to model their interactions with each other.

For example, the Standard Model does not model the exact generating and overcoming cycles of the Five Elements. Instead, mathematically, pairs of elements are opposite of each other and cancels each other -- i.e. water with fire, wood with metal -- at least these are overcoming relationships.  Their interactions with each other are limited, as they represent different axes.  For instance, while water generates wood in the Five Elements, water and wood has no direct interactions in the Standard Model.

In practical applications of the Gan and Zhi cycles to analyze Five Elements, it is common to primarily consider patterns formed by the zhi vectors first and foremost, disregarding the generating/overcoming impacts. Only when all such patterns are considered should the resultant vectors and stand-alone vectors (which do not participate in any pattern) are considered via the elements in a classical Five Elements manner.

As will be seen in later entries, the Standard Model combines all zhi vectors into one resultant vector (which should only represent up to three elements, mapping to the three axes in the Five Elements Phase Space). These three elemental components are then combined with the Gan items, if any, and interpreted via generating/overcoming analysis.

Fixing the Z Component

The 3-Union and 3-Fusion patterns strongly suggest that the Z-axis components of the vectors forming those patterns will cancel out in magnitude and direction, meaning that there are only two possible ways to fix the third dimension on each zhi vector and still be symmetric. The first possibility, the preferred, has the 3-Union and 3-Fusion patterns resulting in vectors with no Z components (red = negative Z, green = positive Z):

Another possibility has the 3-Union and 3-Fusion patterns resulting in vectors with non-zero Z components (red = negative Z, green = positive Z):

The first possibility is preferred as it is completely symmetric, but the second possibility also has certain attractiveness -- in particular, they can be generated by a great circle on a quaternion hypersphere, as show in the next entry!

The Five Elements -- Fundamental Properties

It is uncertain when the concept of the Five Elements was invented, but all evidences pointed to the fact that the concept was very ancient indeed.

The Five Elements are: Metal, Wood (or Air/Wind), Water, Fire, Earth.

Incidentally, in Western cultures going way back to ancient Greece, there were talks (e.g. by Aristotle of around 350BC) describing the Four fundamental Elements of nature -- Water, Fire, Wind, Earth. Sometimes the element "Metal" is blended into "Earth" in Western cultures.

Notice that both Eastern and Western cultures seemed to invent their four/five elements at roughly the same times -- ancient Greece and the "Spring/Autumn" and "Warring States" periods in China.  This period in human history appears to be uniquely fertile for conceptual thoughts.

In China, the Five Elements were used broadly to categorize everyday objects and scientific items.  For example, the first five planets in the solar system were named with the Five Elements. Chinese medicine categorized all herbs and plants under each of the Five Elements, as well as all human organs and all sicknesses.

In fact, "Five Elements" is not a literal translation of the Chinese concept, which should more accurately be translated as the "Five Movements" (or "Five Phases", "Five Agents" in other literature). The strong emphasis on dynamics in Chinese fortune-telling is once again evident here. It is also possible that the Chinese name came from mapping the five elements to the first five visible planets in the solar system -- with the Chinese term for planets being "Moving Star".

Generating and Overcoming Cycles

A unique property of the Five Elements conceptual framework developed in China, as opposed to the four elements in Western societies -- and perhaps the underlying reason for this framework's longevity -- is the idea of "generating" (also known as "benefiting") and "overcoming" (also known as "harming").

Each element of the Five Elements "generates" another element in a predictable cycle:

... Metal generates Water generates Wood generates Fire generates Earth generates Metal...

The ordering of the Five Elements is usually represented in a cycle in the Generating Order (depicted clockwise):

In addition, each element in the Five Elements "overcomes" another element, which is defined as the element one after its next element in the Generating Order:

... Metal overcomes Wood overcomes Earth overcomes Water overcomes Fire overcomes Metal...

The Relationships

For each element in the Five Elements, there is one element that it generates (the one after it in the Generating Order) and one element that it overcomes. In addition, there is one element that generates it (the one before it in the Generating Order) and one element that overcomes it.  Together, the generate/overcome/generated-by/overcome-by properties represented the unique relationships of each elements with the other four elements.

These relationships are so important that there are names given to each relationship:

Same element = 兄弟 (siblings, essentially one's peers, or oneself)
Generates = 子孫 (children, essentially beneficiaries)
Overcomes = 妻財 (wife/wealth, essentially things under one's control)
Generated by = 父母 (parents, essentially benefactors)
Overcome by = 官鬼 (authorities/demons, essentially things that have control)

Relationships are used wide in Chinese fortune-telling by mapping the object or issue under question into one of the five categories, and this creates the extremely important concept of 用神 (applicable or target relationship). For example, when questioning things related to money (which is categorized as things under one's control), one first obtains a "base" element (via various methods), then make predictions based on the element which is "overcome by" the base element.  Essentially, the element overcome by the base element is the 用神 (target), and the base element is the 原神 (source). If, however, the question is related to one's career, the element which "overcomes" the base element will be used as the target instead.

Therefore, a unique application of the Five Elements with regards with fortune telling is not by categorizing question types under each of the five elements, but under each of the five possible relationships.  Predictions are then generally made by inspecting the actual value of the "target" element and whether it is enhanced or subdued by external forces.

Applications of Relationships in Other Fortune-Telling Systems

The importance of using relationships instead of the five elements cannot be emphasized enough.

Many Chinese fortune-telling systems use a disguised form of relationships.  For example, the Ziwei Nubmers system divide a circle into 12 equal houses, but bases most predictions regarding career/business, for example, on the "Careers House", which is located 120 degrees off the "Base House". Predictions regarding money, however, are looked at in the "Money House", which is located 120 degrees off the "Base House" in the opposite direction.  These two relative positions map roughly (although not perfectly due to angle differences) to the "overcome-by" and "overcoming" positions in the Five Elements.

 As will be seen in future entries, many other systems (e.g. the Four Pillars) use a relative -120 degrees from the basis vector to look into fortunes for career/business, and +120 degrees for monetary issues.

A Small Summary on the Bagua

What We Know So Far...

• The eight Bagua trigrams appear to form the group Z8
• The 64 hexgrams appear to form the group Z2 x Z4 x Z8
• In ancient fortune telling, trigrams were generally not used, but hexgrams were formed by random tossings of yallow sticks, with particular lines marked as special (i.e. those with the numbers 6 and 9) -- or in motion (動)
• The I-Ching consists of fortunes for each line in motion for a particular hexgram formed

What We Still Do Not Know...

• Under what kind of procedure are the line patterns of the Bagua trigrams and hexgrams manipulated that can reflect their group theoretical properties -- this particular form of representation (i.e. solid and broken lines) must serve some kind of purposes...
• Formal relationship between trigrams and hexgrams, if any
• Why Jing Fang divide the 64 hexgrams into his particular arrangement of eight houses -- in particular, why the seven generation patterns are chosen

Moving Forward...

Fortune telling based on the I-Ching took the ancient form at least until around 50BC, when the scholar Jing Fang revolutionized the field by merging it with another concept -- the Five Elements, in particular that of the Gan/Zhi (i.e. trunk and branch) cycles, which form a calculus on the Five Elements.

Just as a reminder, the Bagua trigrams are mapped to the Five Elements in the following way:

The order of trigrams shown is the Binary Order -- an ordering invented only in the Sung dynasty (around 1000AD), or almost 1,000 years after Jing Fang merged the Bagua with the Five Elements and revolutionized fortune-telling techniques.

The 64 Hexgrams are Z2 x Z4 x Z8

64 Hexgrams Grouped into Eight Houses

As seen in the previous entry, the eight Bagua trigrams have interpretations in each of the possible groups of order eight. Nevertheless, one must consider the vital fact that the I-Ching never directly refers to trigrams, but instead to hexgrams.

Traditionally, hexgrams are interpreted as two trigrams stacked on top of one another -- and the names of these two trigrams are used as memory aids to the individual names of each hexgram (e.g. 風山漸 means that the two trigrams 風 (巽) and 山 (艮) together form the hexgram named 漸, with 風 on top of 山).

In the Han dynasty (around 50 BC), a scholar of the name Jing Fang (京房) revolutionized the study of the I-Ching by merging the hexgrams with the concepts of the Five Elements as well as the Gan (干, or "trunk") and Zhi (枝, or "branch") cycles. His method formed the basis of the current standard fortune telling technique that yield much more detailed information than previously using only the 64 hexgrams.

The first step in Jing Fang's method is to divide the 64 hexgrams into eight houses. His method of dividing the hexgrams is novel and sheds light on the structure of the hexgrams themselves.

The houses are formed by first taking the eight hexgrams with the same upper and lower trigrams -- these eight hexgrams can potentially form a sub-group that is isomorphic to the Bagua group. This set is called the Basis set.

Each of the eight hexgrams is thus modified in a predictable manner through seven generations (or variations).  The logic of each generation is easy to discern by inspecting the lines of the hexgrams, and they are:

First generation: The lowest line of the base hexgram flipped
Second generation: The two lowest lines of the base hexgram flipped
Third generation: The three lowest lines (i.e. the lower trigram) of the base hexgram flipped
Fourth generation: All but the top two lines of the base hexgram flipped
Fifth generation: All but the top line of the base hexgram flipped
Sixth generation: The fifth line (from the bottom) and the lower trigram of the base hexgram flipped
Seventh generation: The fifth line (from the bottom) of the base hexgram flipped

Notice the sixth and the seventh generations (variations) as they have special names (遊魂 and 歸魂,, the Wandering Spirit and Returning Spirit respectively) and special significance in Jing Fang's fortune telling technique.

The Seven Generations as a Change Group

It is immediately obvious that the seven generations (variations), plus the identity, may form a group representing change of the hexgram lines. In particular, each generation modifies the base hexgram such that, when the top trigram is compared with the bottom trigram (which should be identical in the base hextram), the two trigrams have different lines in different positions based on the generation in question.

As there are three lines in each of the top/bottom trigrams of the base hexgram, there are eight possible combinations of differences of the three lines (counting identity as one).  It can be seen that each of the seven generations, plus the identity, map directly to one combination.

For example, the first generation has the lower line different between the top and bottom trigrams.  The second generation the lower and middle lines. The third generation with all three lines different. The fourth generation, has only the top two lines different, whilst the fifth generation has only the top line different. The sixth and seventh generations are have the middle line different and the top/bottom lines different respectively.

To illustrate with a 3D model:

Notice that, in the 3D representation of this change group, the two most important generations (sixth and seventh) reside on opposite ends of the cube and form the two end-points of the diagonal traversal. Otherwise, the group elements traverse the cube one edge at a time.

Note: This begs the question that whether the seven generations should have been reordered such that all traversals of the cube occur one edge at a time, such as 0 -> 1 -> 2 -> 3 -> 6 -> 5 -> 4 -> 7.

Reconciling The Houses With The 雜卦傳

Unique among the various commentaries of the I-Ching is the 雜卦傳 (Ad Hoc Commentaries on the Hexgrams), an ancient document that focuses on the differences between hexgrams, and their symmetries, both in structure and in meaning.  This document is most crucial in discerning the meaning of each hexgram (other than the hexgram's name) and is frequently quoted, as the I-Ching itself does not make the meaning of each hexgram clear.

The 雜卦傳 matches many hexgrams into pairs, most of them with opposite meanings (but not all). The pairs are constructed by flipping each hexgram upside-down to find its inverse -- thus immediately suggesting an abelian group in operation.  Hexgrams which look the same when flipped upside-down are paired with their mirrored images (i.e. the hexgram formed by flipping each line of the original hexgram from solid to broken and vice versa).

One important feature of the 雜卦傳 is that it does not pair all the hexgrams in a similar manner -- for example, eight hexgrams (姤, 既濟, 未濟, 夬, 大過, 頤, 漸, 歸妹) are not paired for unknown reasons.  Another remarkable feature is that, although many of the meanings cited by the document are opposite in pairs, some pairs are described by meanings that are not clear opposites of each other, some may even be unrelated.

These features suggest that the 雜卦傳 was merely an ancient attempt to make sense of the group structure of the hexgrams by using two inverse-finding techniques -- i.e. flipping upside-down and mirrored image. These techniques failed for those hexgrams that do not follow these two patterns (as seen later), and the author was not able to reconcile them.

The Basis Set is Z8

If one looks at the change group used to crate the seven generations, another characteristic immediately pops out -- the first generation is related to the fifth generation, whilst the second generation is related to the fourth generation. The third generation relates to itself. The relation is that of flipping the lines changed upside-down (thus changing the lowest line becomes changing the topmost line) and taking a mirrored image (thus a line changing becomes non-changing and vice versa).

For example:

It is thus possible to reconcile the methods used by the 雜卦傳 with Jing Fang's houses if we choose a group for the basis set that maps a trigram to its inverse which is the mirrored image or its flipped upside-down version -- or Z8 as discussed in the previous entry!

If Z8 is chosen as the group for the basis set, then hexgrams the first 5 generations (plus the identity) are all automatically paired with hexgrams that are upside-down versions of themselves, except for the houses 乾 and 坤, which are paired with hexgrams within their own houses (since 乾 is the identity and 坤 is -1, self-inversed, in Z8). This discrepancy is perhaps one of the reasons for the difficulties encountered by the author of 雜卦傳, together with another discrepancy which concerns the last two generations.

The Change Group is Z2 x Z4

Judging from the first five generations and their inverses, it is obvious that the change group can only be either Z8 or Z2 x Z4.

The last two generations are more difficult to map, as they do not follow the pattern of the first five generations, simply because they concern trigrams with either the middle line or the top/bottom lines different. In either case, flipping the changes upside-down yields the exact same item, and thus it is not possible to form an inverse-pair in the same manner as the first five generations, since both would have the same lines that are different.  Because of this, it is strongly likely that the last two generations are self-inverses, similar to the third generation.

Another strong support for the last two generations being self-inverses has to do with a few hexgrams that are not in the basis set but still are the same when flipped upside-down -- i.e. 中孚, 頤, 大過, 小過. All such trigrams occur in the sixth generation. In particular, the names of the two hexgrams 大過 and 小過 (literally, "over-large" and "over-small") suggest that they are related, and if treating the last two generations are self-inverses, these hexgrams are paired with each other as inverse-pairs: 中孚 with 頤, 大過 with 小過 (which can also be interpreted as "plus" and "minus").

Therefore, it is concluded that the most likely group for the change group is Z2 x Z4.

I-Ching is Z8 x Z2 x Z4

It is now possible to reconcile the group structure of the 64 hexgrams with interpretations given in the 雜卦傳:

In this diagram:

Blue = Hexgrams not paired by the 雜卦傳

Yellow = Hexgrams paired (correctly or incorrectly) by the 雜卦傳 as mirrored images and with opposite meanings

Light Green = Hexgrams correctly paired by the 雜卦傳 with opposite meanings
Dark Green = Hexgrams correctly paired by the 雜卦傳 but with meanings that are not opposites

Light Red = Hexgrams incorrectly paired by the 雜卦傳 with opposite meanings
Dark Red = Hexgrams incorrectly paired by the 雜卦傳 and with meanings that are not opposites

As can be seen clearly, the author of the 雜卦傳 appeared to get it right on most of the hexgrams, except for the ones in the sixth/seventh generations, as well as those in the 乾 and 坤 houses (which map to inverses within their own houses). Incidentally, six out of the eight blue hexgrams (those not paired by the author) reside in these special-case zones.

A quick look at the meanings of the discrepancies (i.e. red and blue ones) suggests that the "correct" pairings may actually make better sense:

剝 (separate) <--> 逅 (meet/converge)
觀 (observe) <--> 遯/遁 (hide)
夬 (break) <--> 復 (restore)

大過 (delta plus) <--> 小過 (delta minus)
中孚 (reliable) <--> 頤 (middle ground)
隨 (follow, to wed?) <--> 歸妹 (receive/return bride)
師 (make war) <--> 同人 (harmony)

Ones under the "correct" pairings but with meanings less obvious are:

大壯 (strong) <--> 臨 (arrive)
明夷 (harm) <--> 訟 (argument)
漸 (gradual, improve) <--> 蠱 (rot)

Remaining Issue: The Last (Seventh) Generation

The sixth and seventh generators do not follow the same basic formula as the first five generations (six if counting the basis/identity). This is primarily due to the fact that the difference pattern between their upper and lower trigrams are identical when flipped upside-down.

Still, it would appear that the last (seventh) generation could be rendered differently -- for example, having the fifth line (counting from the top) flipped instead of the current second line, or having the forth and last lines (counting from the top) flipped, etc. The hexgrams residing in the seventh generation will be shuffled into different positions, but the group structure will stay valid.

As there are numerous ways to generate seven variations from a basis set which cover all possible difference patterns between the upper and lower trigrams, the rationale behind this particular choice is still unknown, except that it may lead to a consistent procedure (i.e. a calculus) of manipulating the hexgrams that parallel their group-theoretical behaviors.

Bagua is a Group, Most Likely Z8

Binary Interpretation

The Bagua consists of eight trigrams mapping one-one to the eight integers between 0 and 7 representable with three binary bits

Bagua trigrams are also commonly manipulated -- meaning that they can morph from one trigram into other trigrams based on specific rules.  These manipulations, however, do not appear to be numeric in nature -- in other words, the manipulations of trigrams (with operations like flipping a bit -- turning a broken line into a solid line and vice versa) do not map closely to integer arithmethic.

Group Theoretical Interpretation

If one treats the bagua trigrams as a group, however, the manipulations appear to make more sense.  All the requirements of groups appear to match well with the characteristics of the bagua:

• The eight trigrams are mutually exclusive
• The eight trigrams are collectively exhaustive and closed (i.e. there is no possible trigram outside the eight)
• Manipulations of trigrams yield other trigrams
• There is a trigram mapping to identity (most possibly 乾 ☰ or 坤 ☷)
• There is an inverse to each trigram (negative image, flipped, etc.)
• There is an ordering of the 64 hexgrams into an 8x8 matrix (分宮卦序) used in the Four Pillars system, with columns matching the bagua trigrams (shown below) and rows definitely not matching, which almost begs to suggest that the 64 hexgrams is the product of two non-identical groups of order 8 (although it can obviously be also made out of the Cartesian product of two identical groups)

Possible Groups With Order Eight

There are only five groups with order eight up to isomorphism:

• Z8 -- cyclical group
• Z2 x Z4 -- cyclical version of dihedral group
• E8 or Z2 x Z2 x Z2 -- elementary abelian group
• D8 -- dihedral group of eight
• Q8 -- quaternion group

Let us look at all five possibilities in turn.

Trigram Inverses

Classical literature often refer to the inverse of a bagua trigram, almost as if the bagua is a group.  There are two primary systems to describe the negative or inverse of a trigram:

• Flipping all the lines
• Flipping the trigram upside-down (i.e. the first line becomes the last and vice versa, with the middle line staying put)

Flipping all the lines is an obvious way of matching a trigram with an inverse.  Under such a system, each of the three lines in a trigram can be interpreted as independent of each other, like three orthogonal axes (with the eight bagua trigrams on the eight corners of a cube).

Turning the trigram upside-down to find its inverse is also an extremely interesting idea, not merely due to the fact that it is outlined in I-Ching's 雜卦傳 (the one document primarily concerned with inverses), which pairs up the 64 hexgrams as inverse pairs, and most of them are upside-down versions (e.g. 比 and 師, 損 and 益, 震 and 艮).

The "upside-down" concept of finding inverse is also apparent if one treats the three lines in a trigram as three operations to be performed one after another, and if the operation of each line is its own inverse -- which means that the inverse of the combination operation resulting from the three trigram lines is merely the three same operations applied in reverse (and thus flipping the trigram upside-down).

These two possible manners of finding an inverse of a trigram may shed light towards the group structure of the Bagua.

Z8

The simple cyclical group of order eight has one element (say `a`) that generates the entire group:

`a`, `a^2`, `a^3`, `a^4`, `a^5`, `a^6`, `a^7`, `a^8 = e`

It immediately suggests the Binary Order, with 1 being the generator and group product being addition modulo 8 and the identity element being 0:

☰ = `e` (0)
☱ = `a` (1), inverse = ☷ (`a^7` or 7)
☲ = `a^2` (2), inverse = ☶ (`a^6` or 6)
☳ = `a^3` (3), inverse = ☵ (`a^5` or 5)
☴ = `a^4` (4), self-inverse
☵ = `a^5` (5), inverse = ☳ (`a^3` or 3)
☶ = `a^6` (6), inverse = ☲ (`a^2` or 2)
☷ = `a^7` (7), inverse = ☱ (`a` or 1)

It is obvious that this mapping of trigrams to group elements is not attractive, as there is no apparent relation between pair trigrams (e.g. ☰ and ☷, ☲ and ☵ etc.). It is probably because of this that the Binary Order of trigrams was not invented until much later in A.D.

Another mapping of Z8 to trigrams, however, suggests itself, based on the Sibling Order. Notice that `a^4` is its own inverse, and if we map 坤 ☷ to `a^4` we get the following:

☰ = `e` (Father)
☶ = `a` (Youngest son), inverse = ☴ (`a^7`)
☵ = `a^2` (Middle son), inverse = ☲ (`a^6`)
☳ = `a^3` (Eldest son), inverse = ☱ (`a^5`)

☷ = `a^4` (Mother) = -1, self-inverse
☱ = `a^5` (Youngest daughter), inverse = ☳ (`a^3`)
☲ = `a^6` (Middle daughter), inverse = ☵ (`a^2`)
☴ = `a^7` (Eldest daughter), inverse = ☶ (`a`)

Some attractive features of this mapping:

• There are clear choices for the father and mother trigrams (which map to the two most important pure trigrams among the eight)
• The inverse of each trigram is the negative image (i.e. flipping each line) of itself flipped upside-down
• Each trigram is related to one other trigram which has all the lines flipped by the factor -1 -- i.e., any trigram multiplied by ☷ yields its negative image

Z2 x Z2 x Z2 or E8

The elementary abelian group of order eight is one that maps straight to the trigram representation, with each line mapping to one Z2 subgroup.  However, the interactions form an exclusive-or system, since a broken line may map to `a` and a solid line to `a^2`, with `a^2 = e`.  The broken line is thus a generator, meaning one broken line applied against another broken line yields a solid line, with the following multiplication table:

broken x broken --> solid
broken x solid --> broken
solid x broken --> broken
solid x solid --> solid

In other words, all trigrams are self-inverses, and that applying one trigram to another merely flips all the lines in the first trigram where the second trigram has broken lines, and 乾 ☰ is e (i.e. 1,1,1) and 坤 ☷ is (-1,-1,-1).

Z2 x Z4

On the surface, the group Z2 x Z4 looks unlikely to be a strong candidate -- it is abelian and cyclical, thus limiting the possibility of complex interactions.

However, this group is almost a one-to-one map against the strange (but ancient) Sibling Order, as shown below:

☰ = `(e, e)` (Father) = `e`
☶ = `(e, a)` (Youngest son), inverse = ☳
☵ = `(e, a^2)` (Middle son), self-inverse
☳ = `(e, a^3)` (Eldest son), inverse = ☶

☷ = `(-1, e)` (Mother) = -1
☱ = `(-1, a)` (Youngest daughter), inverse = ☴
☲ = `(-1, a^2)` (Middle daughter), self-inverse
☴ = `(-1, a^3)` (Eldest daughter), inverse = ☱


Notice the unexpected features of this mapping:

• There are clear choices for the father and mother trigrams (which map to the two most important pure trigrams among the eight)
• The inverse of each trigram is the trigram flipped upside-down (no other group mapping can boast this feature), a concept outlined in I-Ching's 雜卦傳 (another ancient text)
• There are two special trigrams which look the same when flipped upside-down (i.e. fire ☲ and water ☵) -- they are self-inverses, but also mirror each other by a factor of -1
• Each trigram is related to one other trigram which has all the lines flipped (another common inverse algorithm) by the factor -1

Dihedral Group of Eight (D8)

The dihedral group models 90° planar rotations and planar reflections -- usually denoted by `a` and `r` respectively.  A common representation is:

`e`, `a`, `a^2`, `a^3`, `r`, `ar`, `a^2r`, `a^3r`

where `e` = identity, `a` = rotation by 90° and `r` = reflection.

Only two elements are inverses of each other: `a` and `a^3`.  All other elements are self-inverses.
This makes D8 a less attractive candidate group for the bagua trigrams because:

• so many elements are self-inverses
• it is not apparent to suggest which element should be 坤 ☷ if 乾 ☰ is taken as `e` and vice versa
• it is not apparent how to map each of the three lines in a trigram

One possible mapping of the trigrams is:

☰ = `e`
☱ = `r`, self-inverse
☲ = `a`, inverse = ☵
☳ = `a^2r`, self-inverse
☴ = `ar`, self-inverse
☵ = `a^3`, inverse = ☲
☶ = `a^3r`, self-inverse
☷ = `a2`, self-inverse

Under this mapping, fire 火 ☲ and water 水 ☵ are inverses of each other, representing rotations of +90° and -90°.

Multiplication rules based on manipulating solid and broken lines, however, are difficult to come up with.

Quaternion Group (Q8)

The quaternion group is promising. Not only is it non-abelian, it is anti-commutative and thus opens up much flexibility in terms of manipulation.

One possible mapping of the quaternion group is:

☰ = e
☴ = i
☲ = j
☱ = k
☳ = -i
☵ = -j
☶ = -k
☷ = -1

Notice that this mapping has much going for it:

• There are only two elements which are self-inverses, namely 乾 ☰ and 坤 ☷, incidentally the "father" and "mother" trigrams.
• Each quaternion axis is represented by one line -- three of them (i, j, k), three lines for each trigram.
• The inverse of each quaternion axis is simply the trigram with all lines flipped.
• Since the three quaternion axes are related by anti-commutative rules (e.g. ij = k and ij = -ji), the inverse of each trigram makes some sense (i.e. the inverse of each axis is a combination of the other two axes, or e.g. -i = kj, -j = ik, -k = ji)

Multiplication rules based on manipulating solid and broken lines, however, are difficult to come up with.

Groups Mapping Summary

In order to decide which of the five different groupings map to the eight Bagua trigrams (or the 64 hexgrams), it is useful to identify, for each group, how many elements are self-inverses and how many elements are inverse pairs:

Group	Self-Inverses	Inverse Pairs	Abelian?	Anti-Commutative
E8 (Z2 x Z2 x Z2)	8	0	Y	N
Z2 x Z4	4	2 x 2	Y	N
Z8	2	3 x 2	Y	N
D8	6	2	N	N
Q	2	3 x 2	N	Y

Bagua Ordering and The Five Elements

The I-Ching outlines a fortune-telling system based on 64 hexgrams (or 64-gua).  Each individual hexgram is named individually in the I-Ching, but the particular hexgram is also referred to by the two trigrams forming the first three and last three lines of the hexgram respectively.

For example, the hexgram 益 is made up of the trigram of wind 風 (☴) and thunder 雷 (☳), representing the first three and last three lines of the hexgram for 益 respectively.

The I-Ching itself, strangely, avoids referring to trigrams, but only to hexgrams.  This is strange as future scholars all put heavy emphasis on the trigrams as the first level of categorization, almost as if the 64 hexgrams are mere extensions of the 8 trigrams -- a Cartesian product of the trigrams onto itself.  On the contrary, the I-Ching specifically avoids formally connecting the hexgrams with trigrams in this manner, and only seems to use trigrams as a convenient notation to refer to hexgrams.

In a future post, this issue will be investigated further with the concept that the Bagua trigrams form a group, and the 64 hexgrams also forming a group.

The I-Ching also does not specify a particular ordering or sequencing of the trigrams or hexgrams, and subsequently several popular orders have occurred -- simply because they must be ordered somehow to put into writing.

The Binary Order

One particular popular ordering of Bagua trigrams is the binary order, seemingly dated to the Suing (宋) dynasty close to 1000AD.  The ordering starts with the trigram of 乾 with all solid lines and essentially treat each broken line as a 1, and each solid line as a 0, starting with the top line as the least significant bit:

  乾 ☰, 兌 ☱, 離 ☲, 震 ☳, 巽 ☴, 坎 ☵, 艮 ☶, 坤 ☷

The Binary Order With The Five Elements

The Binary Order is interesting since it coincides with the Five Elements quite nicely:

 Notice that the I-Ching itself does not refer to the Five Elements, which is an independent development parallel to the I-Ching.  The Binary Order and the connection of the Bagua with the Five Elements appear to be the result of subsequent scholastic developments.

The Ordering of the Five Elements When Matched with the Bagua

Also notice that the ordering of the Five Elements is different from typical orders.  In typical Five Elements lists, an order following the "beget/benefit" (生) cycle or the "harm" (剋) cycle is used.  The matching of the Bagua Binary Order with the Five Elements yields a third ordering that is neither of those.

However, if one inspects this order closely, one can find that it matches other fortune-telling disciplines closely, namely the 12-Zhi (12 地支) categories in the Four Pillars system and the Nine-Squares Matrix (九宮) in fengshui.  Both of these will be discussed fully in future entries.

Similarities With 12-Zhi

The 12-Zhi categories can be modeled as in the following diagram:

Basically, the Five Elements are distributed in three axes, with metal (金) and wood/wind/air (木) forming one axis and opposing each other, fire (火) and water (水) forming another axis and opposing each other, and earth (土) being its own axis -- divided into wet earth (濕土) and dry earth (燥土), most likely the two poles of that axis.

Rotating anti-clockwise from metal and arriving at the earth axis last yields this particular ordering.

Similarities With Nine-Squares Matrix

The Nine-Squares Matrix used in fengshui has the following matching between the Bagua trigrams and the nine squares:

As can be seen, again going anti-clockwise from metal "sort of" yields this particular ordering of the Five Elements, with the exception that earth is squeezed in between metal and first, as well as between wood and water.

The difference treatments of earth in the Nine Squares Matrix and the 12-Zhi suggest that the Nine Squares Matrix may be a flat projection of a three-dimensional model (i.e. similar to 12-Zhi) with three axes.  This coincides with the fact that, historically, Chinese fengshui was preoccupied with two dimensions -- there being no high-rises in ancient China.

This almost indicates that the Nine Squares Matrix fengshui system of fortune-telling is a two-dimensional approximation of a three-dimensional model.

The Siblings Order

There is yet another popular ordering of Bagua trigrams -- the so-called Siblings Order.  This order is much more historical, dating almost back to the origins of the I-Ching itself:

Parent: 乾 ☰ (father) -- Yang
- Children: 艮 ☶ (youngest son), 坎 ☵ (middle son), 震 ☳ (eldest son)

Parent: 坤 ☷ (mother) -- Yin
- Children: 兌 ☱ (youngest daughter), 離 ☲ (middle daughter), 巽 ☴ (eldest daughter)

Definitions of the siblings are Siblings Order given in 說卦傳 (Documentaries on Trigrams):

乾，天也，故稱乎父；坤，地也，故稱乎母；震一索而得男，故謂之長男；巽一索而得女，故謂之長女；坎再索而得男，故謂之中男；離再索而得女，故謂之中女；艮三索而得男，故謂之少男；兌三索而得女，故謂之少女。
The 乾 trigram signifies the heavens and is thus the father. 坤 signifies the earth and is thus the mother. 震 contains the first solid line, making it the eldest son; 巽 contains the first broken line, making it the eldest daughter. 坎 contains the second solid line, making it the middle son. 離 contains the second solid line, making it the middle daughter. 艮 contains the third solid line, making it the youngest son. 兌 contains the third broken line, making it the youngest daughter.

Incidentally, according to unearthed ancient documents (帛書周易) written on cloth dating back to the Han Dynasty around 200BC, the order of the eight trigrams are also given as the Sibling Order instead of other more modern orders that put 乾 ☰ and 坤 ☷ at opposite ends.

Notice also that, in the Siblings Order, there are more broken lines in trigrams categorized as male (except for the father itself, which has no broken line), and more solid lines in trigrams categorized as female (except for the mother itself, which has no solid lines).  A popular explanation:

陽一君而二民，君子之道也；陰二君而一民，小人之道也。
Yang trigrams have one head and two subordinates  -- which is the way of the good.
Yin trigrams have two heads and one subordinate -- which is the way of the evil.

Another popular explanation, which actually seems to make more sense:

陽卦多陰，陰卦多陽，其故何也？
Yang trigrams have more yin lines, and yin trigrams have more yang lines.  Why?
陽卦奇, 陰卦偶。
Yang trigrams have odd numbers of yang lines.
Yin trigrams have even numbers of yang lines.

This explanation actually coincides with the Bagua Procedure outlined in a previous entry, when odd multiples of 4 yield a solid (or yang) line, and even multiples of 4 yield a broken (or yin) line.

The Siblings Order and Group Theory

The Siblings Order is apparently the oldest, most ancient, and most authoritative ordering, but one that makes very little practical sense. Unless one actually looks at the eight Bagua trigrams (and the 64 hexgrams) forming a group, which is the topic of the next entry.

The group structure of the trigrams/hexgrams also explains why ancient people should invent such a strange ordering, apparently without any practical reason, before inventing other more rational types of ordering. The Siblings Order arises naturally in certain groups of order eight.

On The I-Ching and The Bagua Procedure

The I-Ching

The I-Ching, or the Book of Changes, is one of China's oldest and most ancient surviving texts.  That this text was used for fortune telling is easy to tell from its title -- the study of events in motion or under change. In modern scientific language, it is thus a calculus on dynamic systems, reducing the science of fortune telling to that of predicting how events will change based on certain laws.
In a commentary of the I-Ching named the 說卦傳 (Descriptions of Hexgrams), there is this famous line:

數往者順，知來者逆，是故易逆數也。
The past is positive, the future is negative. Thus, the I-Ching is concerned with negative numbers/calculations.

It is thus clearly stated that the I-Ching is used for making "negative" calculations, or to predict the future. The most authoritative commentary of the I-Ching, the 繫辭 (Bundled Commentaries), has this to claim:

參伍以變，錯綜其數，通其變，遂成天地之文。極其數，遂定天下之象。
Numbers evolve/change and mix with/criss-cross each other (perhaps referring to a procedure or a mathematical formula).
If all such changes are understood (e.g. formulated as differential equations), one can "write the book" on (what will happen in) the heavens and the earth.
As the numbers (formulas) are evaluated/iterated to their end (e.g. fully integrated), all statuses in the world are determined.
生生之謂易... 極數知來之謂占，通變之謂事，陰陽不測之謂神。
The I-Ching is progressive evolution/iteration/change. Fortune-telling is taking numbers (or formulas) and evaluating/iterating them to their ends (e.g. fully integrated) in order to know the future. Events mean understanding all possible changes. That which cannot be predicted by these methods (yin/yang) is God.

This is by far the clearest implication of fortune-telling as a scientific discipline, in a text that appeared perhaps before 1,000BC!  An even more amazing fact is the commentaries' repeated references to the word 數 (numbers, formulas, or referring to mathematics).  The I-Ching itself has no reference to mathematics or numbers in an arithmetical sense; trigrams and hexgrams do not have numbers in them (although one might argue that their formation involves numbers, as described below).

Why, then, should all commentaries attach numbers (or perhaps mathematics) to the I-Ching without any apparent reason at all?  This can only come from the fact that these authors knew the I-Ching to be a mathematical text on the scientific discipline of fortune-telling, and that it outlines a calculus and treats fortune-telling as solving dynamic systems.

The next series of entries will look at the Bagua system of fortune telling outlined in the I-Ching.

The Bagua Procedure

The following procedure is used to form one single gua (or trigram):

1. Start with 50 sticks of yallow grass (大衍之數五十)
2. Throw one away leaving 49 (其用四十有九)
3. The first cycle:
4. Take one stick, and divide the remaining 48 sticks randomly into two piles (分而為二以象兩, 掛一以象三) -- a, b where a+b=48.
5. Take the remainder of each pile divided by 4 (or 4 if zero).  As 48 is divisible by 4, a and b must either both be divisible by 4 or both non-divisible by 4.  Therefore, the two only possible remainders are 4 (both non-divisible) and 8 (both divisible).  (揲之以四以象四時, 歸奇於扐以象閏)
6. The piles that are left, after deducting the remainder, must either total 44 (=48-4) or 40 (=48-8).
7. The second cycle:
8. Repeat steps #4 to #6: divide the remaining 44 or 40 sticks randomly into two piles and take the remainder of each pile divided by 4 (or 4 if zero).  As 44 and 40 are both divisible by 4, the only possible remainders are 4 and 8.  Thus the piles are left must total one of three only possibilities: 32 (=40-8), 36 (=40-4 or 44-8), 40 (=44-4).
9. The third cycle:
10. Repeat steps #4 to #6: divide the remaining 32, 36 or 40 sticks randomly into two piles and take the remainder of each pile divided by 4 (or 4 if zero).  As 32, 36 and 40 are all divisible by 4, the only possible remainders are 4 and 8.  Thus the piles are left must total one of four only possibilities: 24 (=32-8), 28 (=32-4 or 36-8), 32 (=36-4 or 40-8), 36 (=40-4).
11. Divide the resulting pile by 4, yield one of four only possibilities: 6,7,8,9.
12. The even numbers are yin, with 6 being special and marked with an X.
13. The odd numbers are yang, with 9 being special and marked with an O.
14. This concludes the divination of one line out of three that makes up the trigram.  Repeat for two more times to complete the remaining two lines of the trigram.

Diagrammatically, the procedure can be shown as a decision tree:

The Coins Substitute Method

A simpler method was devised subsequently to use three coins instead.  Essentially, each coin of a toss corresponds to each of the three stages in the procedure. A head = -4, tail = -8.  Follow the corresponding branch of the decision tree to reach the ultimate leaf.

Notice that the order of applying the branches (i.e. coin toss results) does not matter -- the same leaf node is reached.  That is because there is only one value that corresponds to any particular combination of -4 and -8.

There are only four possible outcomes of a coin toss regarding three coins:

• Three heads => -4 x 3 = 48 - 12 = 36
• Two heads, one tail => -4 x 2 -8 = 48 - 16 = 32
• One head, two tails => -4 - 8 x 2 = 48 - 20 = 28
• Three tails => -8 x 3 = 48 - 24 = 24

Thus, the coins substitute method is essentially an exact simulation of the trigram-forming procedure.

O and X Lines

In the I-Ching, all divination's are tied specifically to lines marked by O and X (i.e. 36 and 24, or 9 and 6 in terms of multiples of 4).  For example, a hexgram with the fifth line marked by O is named (九五) while that with the fifth line marked by X is named (六五).

Thus, it is seen that only lines that reach 24 or 36 have significance in interpreting a hexgram.

For each line, the probability of reaching 24 is 0.125 (i.e. 1/8), while that of reaching 36 is also 0.125.  Thus, there is a probability of 0.29 to have only one X or only one O in a trigram, or 0.38 to have only one X or only one O in a hexgram.

The probability of having no X (or no O) in a trigram is 0.67, while having no X (or no O) in a hexgram is 0.45.

The probability of having no X and no O in a trigram is 0.42.  The probability of having no X and no O in a hexgram is 0.18.

The probability of having only one X or O in a trigram is 0.42.  The probability of having only one X or O in a hexgram is 0.36.

Thus, the chances of having only one X or O in a hextram is roughly one-third, in addition to 18% chance of having none.  Essentially, the I-Ching deals with this one-third of possibilities.  The fact that the I-Ching does not deal with situations where there are more than one line marked with X or O strongly suggests that there is a method to reduce the n>1 cases to a combination of n=1 cases (where n = number of lines marked with X or O).

Fortune Telling Is Categorization

For many fortune telling systems (especially the ones under consideration by the author), the entire act of telling one's fortune resides in finding which particular category (out of a number of mutually-exclusive, collectively-exhaustive choices) a person's future trajectory is most probably going to lie.

Exampe: I-Ching Bagua

The I-Ching categorizes future trajectories (essentially a person's fortune, which really is nothing but his/her future) into eight possibilities -- the Bagua system of trigrams.

The I-Ching further expands this categorization by doubling up the Bagua trigrams into duplets called the 64 Gua's of hexgrams.

Example: Sun Signs

Western astrology associates a person's inherent personality with his/her sun sign, which is further categorized into 12 possibilities according to the zodiac of the sun's position.

It can be seen in a future blog entry that the 12 sun signs are further decomposed into three orthogonal axes -- energy (i.e. extrovert vs introvert), logic vs intuition, outwards vs inwards (self-centered or public-centered).

Example: The Five Elements

In Chinese fortune telling, the Five Elements are used extensively as a categorization of future trajectories (i.e. Fire, Water, Wind/Wood/Air, Metal, Earth).

Example: Ziwei Numbers

In the system of Ziwei Numbers, fortune is categorized into 14 stars, which, as will be seen in a future blog entry, can be further decomposed into three othogonal axes -- energy (i.e. extrovert vs introvert), logic vs intuition, outwards vs inwards (self-centered or public-centered).

Notice the uncanny similarities between the categorization of personality in the Ziwei Numbers with the corresponding categorization of personality in western astrology.

Purposes of Categorization

One can guess the reasons for such categorizations -- to aid in calculation, especially in an age without calculating instruments (or even writing instruments) and sound knowledge of mathematics.

Another rationale beyond categorizations is to simply interpretation.  Life is complex, and realities are complex.  Any predictive system, to be useful, must use categorizations to aid in forming opinions on possible future outcomes.  Think, for instance, the Myers-Briggs Type Indicator.

Conjecture: Fortune Categorization and the Chinese Remainder Theorem

Notice an interesting phenomenon -- Chinese culture appears to favor prime numbers, or sets of prime numbers that are co-prime with each other.  For instance, 2 (yin/yang 陰陽), 3 (heaven/earth/man 天地人), 5 (five elements 五行), 7 (seven stars 七星), 8 (bagua 八卦), 9 (nine-squares 九宮).

Some Chinese fortune telling systems use several categorizations simultaneously, and in the vast majority of those cases (if not all), the categorizations used are co-prime with each other.

For instance, the Bagua is essentially a categorization based on 2.  Feng Sui is based on the Nine Squares matrix.  The Four Pillars system uses the Five Elements (5) with two further axes of 10 (天干) and 12 (地支), with 10 being 2x5 and 12 being 2x2x3 -- thus the Four Pillars uses categorizations of 2, 3, and 5 respectively.

This brings one to the mystery of the Chinese Remainder Theorem -- a general result about congruences in number theory and especially to the moduli of pairwise co-primes, laid out in a 1247 book by Qin Jiushao (秦九韶), the Shushu Jiuzhang (數書九章, or Mathematical Treatise in Nine Sections).  An earlier form of the theorem was outlined in the third-century book The Mathematical Classic of Sun Tsu (孫子算經).

This theorem, when first revealed, shocked the western mathematics world, as it would take western mathematics centuries later to come up with similar results.  There is also no particular reason why such a theorem is practically needed, since the rest of the materials in both publications cited above deal with arithmetic techniques in practical everyday usage.  Some have conjectured that the theorem was used in fixing calendars -- but there are holes in this argument: firstly, Chinese calendars have never been extremely accurate, and secondly, western civilizations did not need this theorem to formulate their accurate calendars.

The theorem, however, is essential if one is to formulate and use a mathematical model to calculate fortune and future trajectories.  As most fortune telling systems use categorization to indicate results, and if the results from two or more categorizations are available, the theorem is needed to find out the exact value of the result from two or more categories.  Since fortune telling has been an important activity throughout ancient Chinese society, the practicality of this theorem can be well explained if put in such context.

The Mathematical Nature of Fate and Fortune

In this article, I shall attempt to outline some of the more astonishing aspects of the fortune-telling systems that I have studied.

Fate and Fortune follow mathematical laws

Once again, there is entirely no reason for fate and fortune to be describable or predictable mathematically -- they have no reason to be scientific at all.  Isn't it enough for them to be mere superstitions?

However, the fact is that these fortune-telling systems have survived and endured the test of time -- for millennia in some, much longer than many scientific theories.  The fact that there are still many active practitioners using these systems indicates that they may not be mere superstitions, and that predictions generated by these ancient models may actually be correct more times than randomly justifiable.

Many systems following extremely similar laws

Similar as to mathematical constructs; of course the actual terminologies will be vastly different.

This fact is expected if there is one underlying Equation of Fate that all these systems are attempt to model, albeit in different ways.

The Equation of Fate is cyclical

For almost all systems of fortune-telling, the mathematical models are cyclical.

In other words, the phase space trajectories of fortune dynamics are usually limited cycles or tori, and repeats after a certain number of years (e.g. 600 years for Four Pillars and 120 years or 600 years for Ziwei Numbers).  Fate definitions, for the most part, follow the same trajectories, albeit at a different time scale.  Certain systems, such as western astrology, are tied directly with celestial movements and thus completely cyclical.

Now this is an astonishing fact, as there is entirely no necessity for the Equation of Fate to be cyclical.  It can easily take the form of a non-cyclical function and the differences it will make on lives and fortunes may not be altogether apparent.

The fact that fate and fortune follow cyclical mathematical laws is probably the reason behind much of ancient fortune-telling to base their modelling on celestial movements -- which are cyclical, accurate and the best time-keeping pieces in ancient times.  Systems which are not celestial-based may have terms and names based on stars (e.g. Ziwei Numbers), showing a fondness of ancient scholars to equate cyclical natures with celestial phenomena.  Of course, some systems (e.g. Western Astrology) are purely based on celestial movements.

Fate and Fortune follow the same mathematical model

In most of the fortune-telling systems I have studied, the same mathematical equations are used to calculate fate and fortune, although usually the time scales involved are different.

For instance, the Four Pillars equates one month of fate to 10 years of fortune; Ziwei Numbers equates two hours of fate to 10 years of fortune; western astrology use exact times (i.e. the same time scale for fate and fortune).

Once more, this is a shocking fact as there is absolutely no reason why fortune should follow the exact rules as fate, both of them being different things, one of them static and the other dynamic.

I can give a conjecture towards this -- there must be certain deep connections between fate and fortune themselves, perhaps even different manifestations of the same force.  Perhaps the Equation of Fate is fractal and show self-similarity in time scale -- that fortune is merely a longer-time manifestation of a dynamical fate.

And if that is so, and the Equation of Fate is fractal, then why should fate and fortune be predictable at all -- they should all be different depending on how accurate one is to measure the time of birth.  Obviously, for fortune-telling to work, the equation must be stable in time aggregates, but shows self-similarity with regards to time scale.

It is also possible that the Equation of Fate exhibits chaotic properties -- in particular sensitive dependence on initial conditions, causing the life trajectories of two people born minutes apart to diverge more and more through life.  If such is the case, then the phase space trajectory of the Equation of Fate may trend to a strange attractor.

Fate is set at the time of birth

This much is public knowledge.  Nobody, however, seems to appreciate how remarkable this fact is.  Fortune-telling systems across times and cultures, crossing east and west, all base a person's fate upon the exact time of his birth.

What makes the time of birth such a unique measurement point?  Why not the time of conception (although not entirely ruled out)?  Why not a person's weight, complexion, or other physical measurements?  These are still unanswered questions.

Some thing must have flowed, like a constant river, describable with mathematics, that leaves its mark on a person upon the exact moment of time he/she enters the living world.

Another unanswered question is the inconvenient question of time-zones and latitude.  Fortune-telling systems solve this timing issue in different ways, some not at all.